Valve recently released some very interesting stats, including Death Maps, from HL2: Episode 2 and Team Fortress 2. What are Death Maps? Well, here’s one from the Gravel Pit map for TF2:

I can attest to dying (and killing) quite a few times near the C node in the lower-left corner. Looks like I’m not the only one.
As a designer, I find the TF2 stats fascinating – I would have loved to see similar info on how people played Civ4. Obviously, some of the results are unsurprising. Scouts get the most captures by a ratio of 2:1 over the next best class, the Pyro. Snipers get the most kills. Medics get the most assists. The points category has a little more balance as it includes a number of factors, but there is still a big spread between the Sniper’s 67 points/hour to the Engineer’s 41. The big question, of course, is what Valve should do with this info when balancing the game.
The idea of game balance is a tricky one because many people assume that, in a well-balanced game, all options should be equally valid. Rock, Paper, Scissor is the classic example of an “equally balanced” game, and bringing it up allows me to reference Sirlin’s excellent article on why RPS is a terrible game:
A simple rock, paper, scissors (RPS) system of direct counters is a perfectly solid and legitimate basis for a strategy game provided that the rock, paper, and scissors offer unequal risk/rewards.
Consider a strictly equal game of RPS. We’ll play 10 rounds of the game, with a $1 bet on each round. Which move should you choose? It makes absolutely no difference whether you choose rock, paper, or scissors. You’ll be playing a pure guess. Since your move will be a pure guess, I can’t incorporate your expected move into my strategy, partly because I have no basis to expect you to play one move or another, and partly because I really can’t have any strategy to begin with.
Now consider the same game of RPS with unequal payoffs. If you win with rock, you win $10. If you win with scissors, you win $3. If you win with paper, you win $1. Which move do you play? You clearly want to play rock, since it has the highest payoff. I know you want to play rock. You know I know you know, and so on. Playing rock is such an obvious thing to do, you must realize I’ll counter it ever time. But I can’t counter it (with paper) EVERY time, since then you could play scissors at will for a free $3. In fact, playing scissors is pretty darn sneaky. It counters paper—the weakest move. Why would you expect me to do the weakest move? Are you expecting me to play paper just to counter your powerful rock? Why wouldn’t I just play rock myself and risk the tie? You’re expecting me to be sneaky by playing paper, and you’re being doubly sneaky by countering with scissors. What you don’t realize is that I was triply sneaky and I played the original obvious move of rock to beat you.
In other words, there is no such thing as an “equally balanced” game which is still fun and not just random. Instead, fun games tend to have a “free market” of balance, which ebbs and flows based on the desirability of certain decisions. Scouts and engineers are always going to be important because they are, respectively, the purest offensive and defensive classes. Indeed, these two classes are also the two most popular. However, the Spy can use the sapper to destroy an Engineer’s turret pretty easily, and Pyros are good at lighting Scouts on fire. The Heavy gets the most kills but – as a slow mover – is vulnerable to the Sniper, who is in turn is vulnerable to the Demoman’s grenades. And so on.
The key is that the circle is not complete. Many of the counter units – the Demo, the Pyro, the Spy – do not have counters themselves because there is less incentive to play them in a vacuum. In Sirlin’s words, the classes offer “unequal risk/rewards.” If you play an Engineer, and no one on the other side is playing a Spy, your team is going to have great defense. On the other hand, as more and more people pick Engineers, the more attractive the Spy will become. Nonetheless, the most important goal is to have good defense, not to just be able to screw with the Engineers.
So, we are back at the question of what Valve should do with the stats. By definition, the counter units should never be more popular than the classes they are countering. Thus, it’s ok that the Engineer is twice as popular as the Spy. On the other hand, Valve should certainly learn something from these stats… but exactly what is a bit of a mystery.
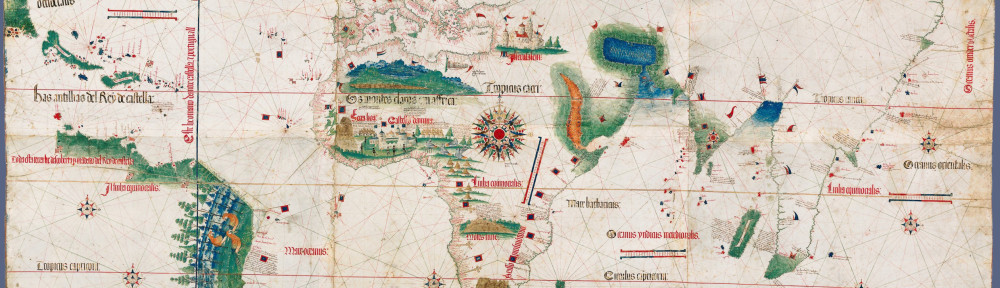
I’m almost worried that it is too much information. The game feels fairly balanced to me, although I haven’t played it all that much. I just hope that they don’t feel they have to tinker just because they have some great telemetry.
From looking at the pic I get a feeling of severe imbalance. It’s obvious there’s only 3 spots to camp, or you’ll be shot by people camping there.
You should expect to see a more even spread than that in a balanced game.
“From looking at the pic I get a feeling of severe imbalance. It’s obvious there’s only 3 spots to camp, or you’ll be shot by people camping there.
You should expect to see a more even spread than that in a balanced game.”
It’s an unbalanced map; there are attackers and defenders. The defenders have to defend the three points, the attackers must capture the three points. In this case, the reason why there are hot spots is because the defenders would logically guard the points and the attackers would logically attack the points. This leads to lots of deaths at the defense points.
I’m curious why blue seems a disproportionate number of times on supposedly balanced maps like 2fort.
Ahhh….. I’ve not played the game, so didn’t know that. 🙂
I do not think that Sirlin is right.
It does not matter what the payouts are: you can always calculate an unbeatable RPS tactic which consists of randomly playing one of the three moves: the payout just determines in which ratio you should play each of the moves. RPS with unequal payouts is just as boring or as interesting as RPS with equal payouts.
Personally, I think RPS is really interesting, even (or especially) with equal payouts. It is true that it is impossible to defeat an opponent which plays one of the three moves completely at random. On the other hand, that particular opponent tactic will not be able to defeat any other tactic. Playing as such is playing for a stalemate.
However, humans play the game differently. Suppose I am playing against you, and my first three moves are paper, paper, paper. You begin to see a pattern, and play scissors the next time. Surprise! I anticipated you seeing a pattern, and played rock!
With humans RPS becomes a game in which you try to see patterns and try to benefit from them. The big problem is that as soon as you are trying to interpret patterns and diverge your playing style from completely random moves, you set yourself up to being exploited by a player who is more clever than you are. RPS is a game of wits.
AI researchers actually use RPS for competitions. It is a simple and pure game. Good AI manages to predict opponents’ moves and hide its own strategy. Purely random play will always be in the middle of the pack: it cannot be exploited, but it will never win either.
For an interesting article on AI RPS tactics, see “Iocaine Powder Explained” by Dan Egnor. I could not find it on the web anymore, but if you search for it with Google you can get it through the Cache.
Rock-paper-scissors (RPS) is balanced, and adding variable payouts does not unbalance the game because you only get paid when you win. To alter the balance, you would need to give players a partial payout for playing, not just for winning. That is, it isn’t enough to tinker with the output–you need to alter the input conditions to see an effect.
A slightly more interesting variant occurs if you decide that a certain choice wins during ties. Consider what happens during Civ IV using its classical era RPS system with unique units thrown into the mix.
The two “weird” factors that creep into the mix are time and cost, because the direct impact on the outcomes isn’t always obvious.
I think you’re partially missing the point, Pieter.
Unequal risk/reward actually removes the “balanced” option of completely random guesses. That is, always playing rock in Sirlin’s example should always win against completely random choices, just because winning with rock is worth so much more than losing. It has the effect of forcing both players to play strategically rather than being able to rely on luck if they choose to do so, such as in the game you described.
The second advantage is that unequal risk/reward creates an “initial state” so to speak, that is, everyone always wants to win with rock, and the other two choices are both simply counters. So, you don’t need to watch me play paper three times in a row before you can decide that a pattern exists, you can actually use information such as the extended history of total matches played by other players of the game to try and guess my move. This has the side effect, by way of a win with rock being worth over 3x more than the next best win, scissors… that you can afford to lose three matches to gauge my ability (provided you never choose scissors, since I’ll then never be able to win with rock), on the hopes that you’ll read my pattern well enough to win with rock shortly thereafter.
Thanks for your response Claytus.
We have a different interpretation of the word “random”. In your interpretation, a random selection between three choices is picking each of them with 1/3 probability.
That is not what I mean by random. For me it is just picking any of three choices, maybe some more than others, but there being no discernable pattern for the sequence of choices.
Example. Suppose the payout for winning with Rock is 2.4, while the payout for scissors and paper is each 0.3. Indeed, an Always-Rock player will score higher than a player that chooses between the three with equal probabilities.
Still, this Always-Rock player will lose from a player who always plays paper, or who chooses randomly between rock and paper with any probability division. So it is certainly not an undefeatable player.
However, examine a player that uses mixed optimal strategies. It plays paper with a probability of 0.8, and the other two with a probability of 0.1. This one will play an even game against your Always-Rock player. It will play an even game against an Always-Paper player. It will play an even game against an Always-Scissors player. It will ALWAYS play an even game. Never better, never worse.
Your Always-Rock player might win from some stupid players, but it cannot win from my mixed optimal strategies player, and it can be defeated easily by a player who has analyzed the pattern (not hard, in this case) and plays always paper. Mine is truly undefeatable. It has exactly the same behaviour as the 1/3-1/3-1/3 player of the standard RPS game.
That is why I am saying that just changing the payoffs does not remove the existence of an undefeatable strategy.
It might be true that introducing unequal payoffs gives people more of an inclination to try out strategies that ultimately prove to be not very good, which they are not prone to do with equal payoffs, as they do not see any direct advantage of preferring one choice over the other.
But the game itself does not become more interesting by doing so.
And it does not need to. It is interesting enough by itself.